Rotating the Bird

Canvas Rotation

Before we jump into rotating the bird, we need to go over how canvas rotation works. When we are drawing to the canvas, the x and y positions are relative to the canvas origin. The origin is located at (0, 0) - the top left corner of the canvas, by default. This is also the origin when we rotate the canvas as well.

The problem with this is we want to rotate the bird around it's center, not the top left of the canvas. Here's an example of a square drawn in the center, rotating around the default origin:

Every frame we rotate the canvas, then draw the square at the center of the canvas. You could imagine this like having a piece of paper with a square sticker in the center. Now put your finger down in the top left corner, and rotate the entire page with your other hand.

What we need to do is change the canvas origin, rotate, then draw. Here's an example of the effect we're after:

To change the canvas origin we can use the translate() method. This method takes two parameters, the x and y position of the new origin. You can probably imagine to rotate the canvas there is a rotate() method. It takes an angle in radians.

Radians to Degrees

Don't worry if you're not familiar with radians for now. We can convert degrees to radians using the following formula:

radians = degrees * (Math.PI / 180)

Here's an example frame() function to demonstrate the example above:

1
const frame = (hrt: DOMHighResTimeStamp) => {
2
  // clear the screen
3
  context.clearRect(0, 0, canvas.width, canvas.height);
4

5
  // move the origin to the center of the canvas
6
  context.translate(canvas.width / 2, canvas.height / 2);
7

8
  // rotate the canvas
9
  // we'll just convert the high res timestamp to seconds since it's
10
  // always increasing (seconds to slow it down)
11
  context.rotate(hrt / 1000);
12

13
  // set the fill color for the square
14
  context.fillStyle = "yellow";
15

16
  // draw the square
17
  // what's up with the negative x and y?
18
  context.fillRect(-25, -25, 50, 50);
19

20
  // "undo" the rotate and translate
21
  context.resetTransform();
22

23
  requestAnimationFrame(frame);
24
};
25

26
requestAnimationFrame(frame);

Let's go over some of the new ideas in this code. We already talked about translate() and rotate(), but why is the fillRect() method using negative x and y values? What is resetTransform()?

After we move the origin to the center of the canvas, we still want to center the square. Positions are relative to the origin. So if we want to draw a 50px by 50px square at its center, we can use -(width / 2) and -(height / 2) for x and y respectively. Remember when we draw images, the position we draw at refers to a point where we will place the top left corner of the image. By subtracting half the width and height, we are moving the image so it's center is at the center of the canvas, the new origin.

Lastly, we need to reset the canvas transform after we're done translating and rotating. This is done by calling resetTransform(). We need to do this because the canvas is stateful. When we apply transformations, they are remembered. We reset the transform each frame to reset assumptions about where the origin is. For example, when we do something as simple as clearing the canvas, we use context.clearRect(0, 0, canvas.width, canvas.height). If we didn't reset the transform, that (0, 0) point would refer to the center of the canvas. This would cause us to only clear the bottom right quadrant of the canvas!

Canvas Transformations

This is not the only way to transform the canvas. We also simplifed the explanation a little. Underneath we are modifying a Matrix (DOMMatrix) object. This object is a 2D matrix (think grid) that represents the current transformation of the canvas. We don't need to dig into the details of this to achieve our goals, but it's useful to be aware of.

See the docs for more information.

Rotate the Bird

If we imagine due East being 0 degrees, we're going to allow the bird to look upward a maximum of 25 degrees, and downward a maximum of 50 degrees. In this scenario upward is negative and downward is positive.

Let's use the crudest version of this we can, and just set rotation to one of these two extremes where appropriate. If velocity is positive, the bird is falling and needs to look down. If velocity is negative, the bird is rising and needs to look up.


1
export class Bird {
2
  // ...
3
  velocity = new Vector2d();
4

+
  /**
+
   * Rotation in degrees
+
   */
+
  rotation = 0;
9

10
  // ...
11

+
  public setRotation() {
+
    if (this.velocity.y < 0) {
+
      this.rotation = -25;
+
    } else if (this.velocity.y > 0) {
+
      this.rotation = 50;
+
    }
+
  }
19

20
  public update(delta: number) {
21
    switch (this.state) {
22
      case BirdState.Idle: {
23
        this.flapAnimation.update(delta);
24

25
        break;
26
      }
27

28
      case BirdState.Flying: {
29
        this.flapAnimation.update(delta);
30
        this.velocity.y += this.gravity * delta;
31
        this.position.y += this.velocity.y * delta;
+
        this.setRotation();
33

34
        break;
35
      }
36
    }
37
  }
38
}

Now that we're storing rotation, let's apply the transformation and draw the bird:


1
class Bird {
2
  // ...
3

4
  public draw(context: CanvasRenderingContext2D) {
+
    context.translate(this.position.x, this.position.y);
+
    const rotation = (this.rotation * Math.PI) / 180;
+
    context.rotate(rotation);
8

9
    const currentFrame = this.flapAnimation.getCurrentFrame();
10

11
    context.drawImage(
12
      this.spriteSheet,
13
      currentFrame.sourceX,
14
      currentFrame.sourceY,
15
      currentFrame.width,
16
      currentFrame.height,
+
      -currentFrame.width / 2,
+
      -currentFrame.height / 2,
19
      currentFrame.width,
20
      currentFrame.height
21
    );
22

+
    context.resetTransform();
24
  }
25
}

We're making use of the points we discussed earlier:

Set the origin to the position of the bird
Convert the rotation to radians
Rotate the canvas
Update the destination x and y values of be half the width and height of the bird respectively
Reset the transform

Great! Now let's make it better because this is really not the end result we're after.

Rotate Based on Velocity

We want the rotation to be smooth as it transitions from upward to downward. To achieve this we'll make it based on the birds velocity and thrust.

Let's start with the rotation downward right after the bird flaps and begins falling towards a velocity of 0. We said 25 degrees is the maximum rotation looking upward, but that will really be -25 since we need a counter clockwise rotation from 0 (East). Let's use Math.max() to make sure the rotation is never smaller than -25 degrees. Remember, Math.max(-25, 0) would result in 0 because the larger number is the number closer to 0.

The problem is what will be the second argument we pass to Math.max()? Let's turn this into a percentage problem, but as a fraction: from 1 to 0. With a fraction we can multiply it by any target value to find out how far along we are. For example, 50 / 100 = 0.5. If we multiply that by -25, we get -12.5 or half our rotation towards 0.

When we click the mouse, we set the velocity to the value: -thrust. This is our max thrust. So if we want to turn that into a fraction of our rotation, we can use -maxRotationUpward * (velocity.y / -thrust). So what's happening here is we're going to start at full rotation upward because our fraction of velocity is 1 (100%). As gravity pulls the bird down, the velocity will decrease causing the fraction to decrease towards 0. This gives us a nice transition over time.

This diagram may help visualize this:

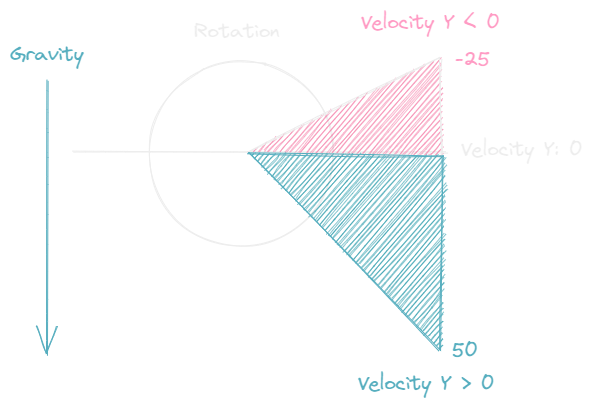
Let's update our setRotation() method to account for this change:


1
export class Bird {
2
  public setRotation() {
3
    if (this.velocity.y < 0) {
+
      this.rotation = Math.max(-25, -25 * (this.velocity.y / -this.thrust));
5
    } else if (this.velocity.y > 0) {
6
      this.rotation = 50;
7
    }
8
  }
9
}

If you play the game now you'll notice a nice smooth rotation after the thrust until the bird looks due east. After that it snaps straight down.

We need to apply the exact same technique for a positive velocity. We'll use Math.min() to make sure the rotation is never larger than 50 degrees.


1
export class Bird {
2
  public setRotation() {
3
    if (this.velocity.y < 0) {
4
      this.rotation = Math.max(-25, -25 * (this.velocity.y / -this.thrust));
5
    } else if (this.velocity.y > 0) {
+
      this.rotation = Math.min(50, 50 * (this.velocity.y / this.thrust));
7
    }
8
  }
9
}

There you have it! Nice smooth rotation. The bird movement is feeling much better now.

In the next section we'll talk about collision and start by having the bird collide with the ground.