Circle VS Rectangle Collision

Collision Detection VS Resolution

Before we get into collision let's talk about detection and resolution. Collision detection is the process of determining if two objects are intersecting/overlapping. Collision resolution refers to how we handle a collision event. For example, in a platformer game we'd detect a collision when the player descends from a jump and lands on the ground. This means the player has moved into the ground within a game loop frame for the detection to be true, and we now need to push them back up so they are no longer overlapping.

In this game we will not be addressing collision resolution. When the bird hits a pipe or the ground and "sinks" into it, we're going to leave it for visual effect. The reason is because when collision occurs we want it be very visually clear, and we're going to stop the game to restart on click anyway.

How it Works

We need to determine the distance between two points: the circle's position and some point along the rectangle's edges. We'll be using Pythagoras' theorem and the hypotenuse (or distance) to determine if a circle and rectangle are overlapping. As a reminder, to determine the hypotenuse (c) the formula is: c = sqrt(a² + b²).

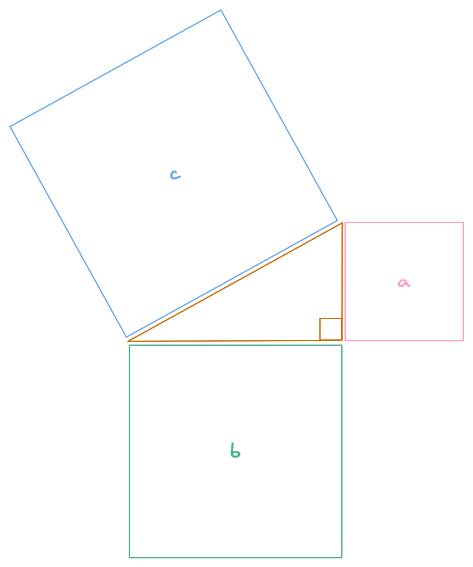
Given two points, we can determine the length of sides a and b to complete the formula. We already have the position of the circle at its center. We need to determine a test point along the rectangle's edges. We have 8 possible points of interest: the 4 corners, and one along each edge.

To start we'll use the circle's position as the test point. Then we'll perform a series of circle-to-edge comparisons to determine the most approriate x and y values for the test point. This sounds more complicated than it is. Here's a code segment to demonstrate:

1
// our test point, start with the circle's position
2
let testX = circleX;
3
let testY = circleY;
4

5
if (circleX < rectangleX) {
6
  // left edge
7
  testX = rectangleX;
8
} else if (circleX > rectangleX + rectangleWidth) {
9
  // right edge
10
  testX = rectangleX + rectangleWidth;
11
}
12

13
if (circleY < rectangleY) {
14
  // top edge
15
  testY = rectangleY;
16
} else if (circleY > rectangleY + rectangleHeight) {
17
  // bottom edge
18
  testY = rectangleY + rectangleHeight;
19
}

We started by copying the circle's postition to the test point because we won't always update both the x and y values of the test point. That only happens if the circle is in a quadrant that contains one of the corners of the rectangle. For example, circleX < rectangleX && circleY < rectangleY would put us in the top left quadrant. When the circles center is not in one of these 4 colored quadrants we only need to update the test point's x or y value depending on which edge it's along.

Here's a diagram to help visualize this:

The orange etched sections are the quadrants that would contain one of the rectangles corners. If the circle is outside of those quadrants, it must be along one of the edges.

Circle VS Rectangle Intersect Helper

Let's add a helper function to determine circle vs rectangle collision.

src/lib/collision.ts
1
export const circleRectangleIntersects = (
2
  circleX: number,
3
  circleY: number,
4
  radius: number,
5
  rectangleX: number,
6
  rectangleY: number,
7
  rectangleWidth: number,
8
  rectangleHeight: number
9
) => {
10
  // our test point, start with the circle's position
11
  let testX = circleX;
12
  let testY = circleY;
13

14
  // which edge is closest?
15

16
  if (circleX < rectangleX) {
17
    // left edge
18
    testX = rectangleX;
19
  } else if (circleX > rectangleX + rectangleWidth) {
20
    // right edge
21
    testX = rectangleX + rectangleWidth;
22
  }
23

24
  if (circleY < rectangleY) {
25
    // top edge
26
    testY = rectangleY;
27
  } else if (circleY > rectangleY + rectangleHeight) {
28
    // bottom edge
29
    testY = rectangleY + rectangleHeight;
30
  }
31

32
  // get distance from closest edges
33

34
  // length of side a
35
  const distX = circleX - testX;
36
  // length of side b
37
  const distY = circleY - testY;
38
  // hypotenuse
39
  const distance = Math.sqrt(distX * distX + distY * distY);
40

41
  // if the distance is less than the radius, collision!
42
  if (distance <= radius) {
43
    return true;
44
  }
45

46
  return false;
47
};

Demo

Here's an interactive demo that will hopefully help you further understand the code above.

With that out of the way, let's move on to setting up the entities with their colliders.